UNIDAD 3:Elementos básicos de geometría plana.

Construcción de una circunferencia:

• trazar un segmento  (AB)de "x" medida.
• Delimitar un punto
• hacer centro con el compás y medir la distancia del segmento
• trazar la circunferencia.

Conclusión: una circunferencia requiere para su trazo de punto y radio

Construcción de un segmento congruente:

• con ayuda de  regla no graduada, traza una linea en la inclinación que mas te guste/convenga.
• Delimita A1 marcando un punto sobre la linea (donde sea más de tu agrado).
• con el compaz has centro en A y llega a B.
• con la medida del compás has centro en A1 y marca la distancia de B1

Conclusión: la medida y forma de los segmentos trazados son los mismos

Construcción de ángulos congruentes:

Nota: hay que tener en cuenta que los ángulos se miden de forma contraria a la del reloj, osea de izquierda a derecha.

• Teniendo el ángulo ABC,  hacer centro en B y marcar a cualquier punto en AB.
• Marcar por donde pase el punto en BC para obtener E
• Con la regla marcar A1B1 
• En el ángulo ABC tomar con el compás la medida de BD y trazar esa medida en A1B1 
• Transportar la distancia entre BD y marcar D1
• Hacer centro en D hasta E, con esa medida hacer centro en D1 y marcar E1 (hacia la izquierda)
• Trazar B1C1 y ya tienes el ángulo.

Construcción de una bisectriz:

• Teniendo el ángulo ABC, hacer centro con el compás en B hacia cualquier punto en AB para obtener el punto D
• con esa medida marcar en BC para obtener E
• con la medida que se quiera abrir el compás, marcar la circunferencia desde D y también desde E
• de donde cruzan las circunferencias marcadas, trazar un nuevo segmento, el cual llamaremos BF

Conclusión: Los triángulos BDF y AFE son congruentes entre sí.

Construcción de una mediatriz:

• En una linea marcar los segmentos AB.
• Hacer centro en A para B, trazar una circunferencia.
• Hacer centro en B para A, trazar una circunferencia.
• DOnde cruzan las circunferencias trazar un segmento llamado CD.
• en el centro de AB, CD llamamos F, donde F es el punto medio de AB.

Conclusión: la mediatriz pasa por el centro del segmento AB, pero haciendo centro en  cualquier punto entre el segmento CD hacia A la distancia en hacia B es la misma.

Trazo de una recta que divida un segmento en tres partes iguales

• Delimitar en la recta el segmento AB
• Hacer centro en A y abrir la distancia de tres dedos (aproximadamente)
• Con la misma apertura marca otro corte haciendo centro en el primer corte
• Repetir el mismo paso dos veces mas en el nuevo corte
• Trazar una semirecta que pase por A,la llamaremos segmento AC
• Trazar otra recta que pase por B,C
• Con ayuda de la escuadra marcar la recta BC,con otra escuadra o una regla no graduada colocarla debajo de la 1° escuadra
• Retirar la 1° escuadra sin mover la segunda trazar una recta  en el 3° corte,esta linea trazada la llamaremos segmento DF
• Hacer lo mismo en el 2° corte y al segmento trazado lo llamaremos FG

CONCLUSIÓN: los segmentos  BC, DE y FG son paralelos entre sí.

Construcción de una recta que represente la distancia que existe entre un punto P fuera de la recta.

• Hacer centro hacia  el punto P, marcar el corte.
• Hacer centro en P y marcar los cortes que se hacen en la recta.
• Con la misma distancia hacer centro en ambos cortes  y marcar el cruce  del lado opuesto a P.
• Trazar una recta que pase por el cruce y P.

CONCLUSIÓN:la perpendicular pasa por el segmento que representa la distancia más corta.

Construcción  de una recta que represente la distancia que existe entre un punto P dentro de la recta

• Hacer centro en P hacia cualquier punto de la recta, debe cortar ambos lados de la recta.
• En los cortes, trazar un arco hacia ambos lados de la recta.
• Trazar uan recta que pase por los cortes marcados.

CONCLUSIÓN:la perpendicular pasa por el segmento que representar la distancia mas corta 

Construcción de una recta paralela en P cuando este esta fuera de la recta L

• En la distancia mas corta a la recta hacer centro en P,marcar  los cortes que se hagan en la linea.
• Con la misma distancia, hacer centro en A  y trazar un medio arco,el nuevo corte lo llamamos C.
• Hacer lo mismo pero haciendo centro en B.
• Hacer un nuevo arco haciendo centro en C.
• Trazar una recta que pase por P y los demás cruces formados.

 Postulado de las rectas paralelas y su inversa

Para poder entender esto, ,se tienen que trazar dos rectas que se llamarán L1 y L2,y la cortaremos con una secante,seguido esto nombramos dos ángulos formados...

ahora en este caso diremos que son paralelas ,entonces L1 es paralela con L2

• Sólo son parlelas si el ángulo "X" +"Y" = 180°.
• De acuerdo con el postulado, el ángulo "X"+"Y"= menor a 180°se intersectan las rectas a la izquierda.
• El ángulo "X"+"Y"= mayor a 180° se intersectan las rectas a la derecha

Construcción de triángulos equiláteros 

Dos triángulos cuyas medidas se encuentran dentro de una recta en los segmentos "AB", "AC".

• Trazar un segmento con ayuda del compás de ambas medidas de los puntos "AB" y "AC"
• Marcar los puntos de intersección de los puntos (tiene que ser la misma madida

Conclusio: Cuando un triángulo tiene sus 3 lados iguales se llama equilátero

Construcción de triángulos isósceles.

Dos triángulos cuyas medidas se encuentran dentro de una recta en los segmentos "AB", "AC", uno cuya longitud sea = al segmento AB y el tercero l segmento BC, y el 2° con des segmentos iguales al segmento AB yel 3° a AC.

• para el primero se traza una recta, se toma la medida de AB y deja un corte fuera de la recta.
• Del lado donde quedó el rorte, sobre la recta traza con el compás otro corte que pase por el anterior haciendo centro en la recta (donde se cortó el segmento)
• Para el 2°se traza un segmento con la medida de AB,  con esas misma distancia se marca un corte fuera de la recta.
• Con la medida de AC, hacer centro en el en el punto opuesto del corte del segmento, luego se unen los puntos.

Conclusión: Puede haber triángulos isósceles, recto, acutángulo y obtusángulo.

Triángulo escaleno

Dos triángulos cuyas medidas se encuentran dentro de una recta en los segmentos "AB", "AC","AD".uno con las longitudes de los seg. AB, BC, y el otro con las longitudes de los seg. AC, BD, AD. 

• Se traza el segmento AB
  en un punto se hace centro con la medida de BC, en el otro punto con CD
• en donde se cruzan las circunferenciax trazar los segmentos para unir el triángulo.

• Se traza el segemnto BD
• en un punto hacer centro con la medida del segmento AC y en el ootro punto con AD.
• unir los puntos.

Conclusión:Puede haber triángulos escalenos acutángulos y obtusángulo, también rectos.

Desigualdad del triángulo.

La suma de los dos lados más cortos del triángulo debe ser mayor al tercer lado, es decir, el más grande.

A+B>C

Suma de ángulos interiores.

La suma de los ángulos interiores de un triángulo es 18°, sin importar el tipo.

Teniendo un triángulo ABC:

• Prolonga el segmento de cualquier cara del triángulo.
• En el ángulo opuesto al segmento prolongado hay agregar los ángulos interiores restantes al triángulo, de manera que serán angulos suplementarios.

Conclusión:Los ángulos suplementarios formados en el triángulos forman una recta paralela al segmento prolongado.

Suma de ángulos exteriores.

El angulo exterior es el que acompleta los 180°, prolongado una semirecta de cualquier lado de los segmentos del triángulo, todos deben de ir hacia el mismo sentido, ya sea a la derecha o a la izquierad.

• Se prolongan los ángulos exteriores del triángulo.
• Trazar un segmento, en ese segmento trasladar la medida de un ángulo exterior.
• Trasladar los otros ángulos exteriores de manera que van a formar una circunferencia.

Suma de  dos ángulos interiores.

La suma de dos angulos interiores es igual al ángulo exterior no adyacente.
Teniendo un triángulo "ABC", la suma de los ángulos A y B tiene que ser igual al ángulo exterior C... Parara comprobarlo:

• Tienes que trazar un ángulo interior.
• Hacer los mismo con otro ángulo interior acomodándolos uno seguido del otro, de tal manera que compartan un segmento.
• El resultado tiene que ser igual al ángulo exterior del que no se ha utilizado para lo anterior.

Rectas y puntos notables en un triángulo

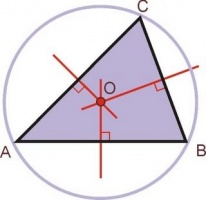
Circuncentro.

• Trazar las mediatríces de cada cara del triángulo.
• El punto de interseccion entre las 3 rectas se llama "circuncentro".
• Haciendo centro en el circuncentro hacia cualquier vértice del triángulo y trazar una circunferencia.

La utilidad del circuncentro es que se puede hacer una circunferencia que pase por los vértices de un triángulo, esta circunferencia se llam "circunscrita".

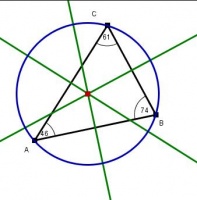
Incentro.

• Se traza obteniendo las bisectríces de cada vértice del triángulo.
• El punto de intersección se llama incentro.
• Haciendo centro en el circuncentrohacia cualquier parte de un segmento, se traza una circunferencia, roza con las 3 caras del triángulo.

Una circunferencia que es tangente a las tre caras del triángulo se llama inscrita.


Baricentro.

• En cada cara del triángulo trazar una mediatríz de manera muy clara, casi inperseptible.
• Marcar el punto de intersección entre la mediatríz y el segmento.
• Trazar un segmento que valla del punto antes marcado al vértice opuesto.

De esta manera sepuede hallar el centro de un triángulo.

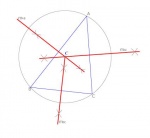
Ortocentro.

Teniendo un triángulo "ABC":

• Hacer centro en A hacia B y en C y marcar los puntos de intersección entre las circunferencias.
• Unir con un segmento el punto de intersección con el segmento no adyacente.
• Hacer centro en B hacia A y C, marcar los puntos de intersección entre las circunferencias.
• Unir con un segemtento el punto de intersección con el segmento no adyacente.
• Hacre centro en C hacia A y B y marcar los puntos de intersección entre las circunferencias.
• Unir con un segemento el punto de intersección con el segmento no adyacente.

El punto de intersección entre los 3 segmentos trazados se llama ortocentro, este nos sirve para conocer las 3 alturas del triángulo.

Glosario.

1. Punto

   
   Etimología de punto

   Origen, historia o formación
   Proviene del latín punctum para referirse a la señal circular pequeña que divide una línea en la escritura.
   https://definiciona.com/punto/

   Geometría y diseño

   • Punto (geometría), ente adimensional que describe una posición en el espacio;en diseño, al punto, la mínima expresión gráfica; nace con el choque de un instrumento (lápiz) contra el plano (soporte), y puede tener forma, color y textura
     
     
     
     
     es.wikipedia.org/wiki/Punto
     
     
2. Linea
   La palabra línea viene del latín linea, derivada de "linum" y ésta a su vez de griego "linon" cosa hecha con lino, hilo de lino. La palabra linea es en realidad en latín el femenino del adjetivo lineus-a-um (de lino). En latín una linea se refería a un finísimo hilo de lino.
   
   http://etimologias.dechile.net/?li.nea
   

   Una línea está formada por una sucesión de infinitos puntos. Puede que os extrañe que sean infinitos puntos lo que la forman porque nuestra percepción visual solo ve un trazo continuo, pero si nos acercamos lo suficiente podemos apreciar que realmente son puntos que se sitúan uno junto a otro.

   
   
3. Linea recta
   
   Sucesión de infinitos puntos (no tiene principio ni fin, es decir no tiene límites) donde los puntos están alineados en una misma dirección.
   Si nos acercamos para ver un trozo de la línea recta con una lupa especial, vemos que efectivamente la línea está formada por puntos.
   
   https://www.smartick.es/blog/matematicas/geometria/lineas-rectas-y-lineas-curvas/
   
4. Semirrecta
   s. f. GEOMETRÍA Cada una de las dos partes en que queda dividida una recta por cualquiera de sus puntos.
   
   https://es.thefreedictionary.com/semirrecta
   
   

   Las semirrectas pueden estar abiertas o cerradas por el extremo que las delimita. El extremo que acaba en infinito o empieza en menos infinito, siempre está abierto (se utilizará el paréntesis para abrir o cerrar).

   Tipos de semirrectas

   Vamos a ver los diferentes tipos de semirrectas:Semirrecta abierta por la derecha

   Una semirrecta abierta por la derecha:

   
   

   

   Es el rango de valores que va desde menos infinito, hasta el extremo a, pero sin incluirlo.Comprende los números menores que a:

   Y se representa de la siguiente forma:

   

   Donde el punto a queda vacío.

   https://ekuatio.com/intervalos-y-semirrectas/
5. Segmento de la linea recta
   
   Un segmento, en geometría, es un fragmento de recta que está comprendido entre dos puntos, llamados puntos extremos o finales.
   Así, dado dos puntos A y B, se le llama segmento AB a la intersección de la semirrecta de origen A que contiene al punto B con la semirrecta de origen B que contiene al punto A. Los puntos A y B son extremos del segmento y los puntos sobre la recta a la que pertenece el segmento (la «recta sostén»), serán interiores o exteriores al segmento según pertenezcan o no a este.
   https://es.wikipedia.org/wiki/Segmento
   

   
   
   
   Segmento AB (en verde) contenido en la recta AB.
   Se caracteriza porque :
   Es una porción o parte de una recta.
   es la menor distancia posible entre dos puntos.
   y por que tiene un principio y un final, por ende es suceptible de ser medido.
   

   http://profesor-matematicas.blogspot.mx/2008/12/segmento-de-recta.html


6. Ángulo
Geometría.
Figura formada por dos segmentos de recta que inician en el mismo punto (ángulo plano) o por tres planos que se interceptan (ángulo solido).

• Derivados: angular, angulado, angularmente, anguloso, angulosidad.

Espacio angular que se forma en la zona interna donde se encuentran dos paredes o dos superficies.


• Sinónimo: rincón.
  
  https://es.wiktionary.org/wiki/%C3%A1ngulo

7. Sistema de medición de ángulos (rados [decimal y sexagesimal] y Radiantes). Cómo convertir de grados en radiantes y de grados decimales a grados sexagesimales.
   
   Para medir ángulos se pueden usar distintos sistemas de medición ellos son:
   

   • Sistema Sexagesimal.
   • Sistema Centesimal.
   
   
   SISTEMA SEXAGESIMAL:la unidad de medida en este sistema es el grado sexagesimal (1º), que se obtiene de dividir el ángulo recto en 90 partes iguales.
   
   
   1º = 1R  => 1R = 90º
                                             90
   Los submúltiplos del grado sexagesimal son el minuto sexagesimal (1') y el segundo sexagesimal (1'').
   1º = 60'    ^     1' = 60''   =>  1º = 3600''
   
   
   SISTEMA CENTESIMAL:  la unidad de medida en este sistema es el grado centesimal (1^G), que se obtiene de dividir el ángulo recto en 100 partes iguales.
   
   
   1^G  =  1R    =>  1R = 100^G 
                                          100
   Los submúltiplos del grado centesimal son el minuto centesimal (1^M) y el segundo centesimal (1^S).
   

   
   

   
   

   1^G = 100^M   ^   1^M = 100^S   ⇒   1^G = 10000^S
   

   http://cristinabollatti.blogspot.mx/p/sistemas-de-medicion-de-angulos.html
8. una clasificación segun su medida es:
   
   A)Ángulo rectoEstá compuesto por dos semirrectas que se unen por un vértice como cualquier ángulo, pero la posición de estos dos segmentos ha de ser perpendicular siempre. Al juntarse dos líneas de forma perpendicular dejan la misma separación entre una y otra, por tanto, la amplitud del ángulo recto es idéntica en cualquier caso.Dicho esto, la medida del ángulo recto será de 90 grados sin variaciones. A diferencia del ángulo agudo, del cual podemos encontrar noventa diferentes, o del ángulo obtuso con multitud de posibilidades también. Lo que hace exclusivo al ángulo recto es que siempre es igual.
   https://es.plusmaths.com/angulo-recto.html
   B)Ángulo agudo
   El ángulo agudo es el espacio entre dos rectas que comparten un mismo vértice cuya inclinación o apertura es mayor que 0 grados (0°) y menor que 90 grados (90°).
   https://www.significados.com/angulo-agudo/
   
   c)Ángulo obtuso
   Los ángulos obtusos se forman de la misma forma que los ángulos agudos o rectos, es decir, mediante dos semirrectas que se unen en un vértice. Sin embargo, se diferencian de ellos en la medida que poseen.
   Los ángulos obtusos son aquellos que valen entre los 90º y los 180º. Para medir ángulos obtusos podemos hacer uso de un transportador de ángulos o mediante la combinación de la escuadra y cartabón
   https://es.plusmaths.com/angulo-obtuso.html
   
   D)Angulo llanoEs el espacio comprendido en una intersección entre dos rectas cuya apertura mide 180 grados o 180º. Como el ángulo es de 180º no hay una diferencia entre dos rectas o una recta y podemos decir que los ángulos en una línea recta siempre suman 180º.
   
   https://www.significados.com/angulo-llano/
   E)Ángulo entrante o cóncavo
   Es un ángulo que oscila entre los 180º y los 360º. Es el segundo ángulo más grande después del ángulo completo.Los ángulos cóncavos también se denominan ángulos entrantes oángulos reflejos. Se llaman así también porque cuando realizamos un ángulo convexo, el ángulo resultante que se refleja por la parte exterior es un ángulo cóncavo.
   https://es.plusmaths.com/angulo-concavo.html
   
   F)Ángulo perígono.
   Es el ángulo en el que uno de sus lados coincide con el otro, formando un arco de una circunferencia y cuyo valor es de 360°.
   
   http://jorge_cetis10.mx.tripod.com/objetivo20.html
9. Otra clasificacion de los ángulos según su posición es:
   A)Opuestos por el vértice
   
   Los ángulos que tienen el vértice y un lado común se llaman "consecutivos".
   
   B)Adyacentes
   Se llama ángulos adyacentes a todo par de ángulos que son consecutivos y suplementarios. Los ángulos consecutivos tienen un lado común y los otros dos lados son semirrectas opuestas.
   
   
   

   https://sites.google.com/site/susanparalela/angulos-consecutivos-adyacentes-y-opuestos-por-el-vertice
   C)Complementarios
   Los ángulos complementarios son aquellos ángulos cuyas medidas suman ${\displaystyle 90^{\circ }}$ (grados sexagesimales), es decir que si dos ánguloscomplementarios son a su vez consecutivos, los lados no comunes de estos forman un ángulo recto.
   https://es.wikipedia.org/wiki/%C3%81ngulos_complementarios
   
   D)Suplementarios
    son aquellos que suman 180º entre los dos ángulos. De esta forma son ángulos suplementarios los que, cuya suma, forma un ángulo llano, es decir 180º. El concepto de ángulo suplementario hace referencia a completar lo que le hace falta hasta que llegar a los 180º.
   
   https://es.plusmaths.com/angulos-suplementarios.html
10. Triángulos
    Es un polígono de tres lados que da origen a tres vértices y tres ángulos internos. Es la figura más simple, después de la recta en la geometría. Como norma general un triángulo se representa con tres letras mayúsculas de los vértices (ABC).
    
    http://conceptodefinicion.de/triangulo/
    

    

    
    
11. Clasificación de los triángulos por sus lados
    · Isósceles: posee dos lados iguales y uno diferente.
    · Equilátero: tiene sus tres lados iguales.
    · Escaleno: posee sus tres lados diferentes.
    http://queenlnf.blogspot.mx/2009/04/clasificacion-de-triangulos-segun-sus.html
12. Clasificación de los triángulos por sus ángulos1) Rectángulos: Tienen un ángulo recto ( 90º).2 Obtusángulo: Tienen un ángulo obtuso (mas de 90º)
    3) Acutángulos: Tienen todos sus ángulos agudos (menos de 90º)
    
    http://es.tareasnormalseis.wikia.com/wiki/Clasificaci%C3%B3n_de_los_tri%C3%A1ngulos_seg%C3%BAn_sus_%C3%A1ngulos
    
13. Rectas y puntos notables en el triángulo
    
    Entre las rectas notables más conocidas de un triángulo se pueden nombrar las mediatrices, las medianas, las alturas y las bisectrices; cada una de estas rectas notables determina cierto punto notable: circuncentro, baricentro, ortocentro e incentro, respectivamente.

    Mediatriz

    Mediatriz: Conjunto de puntos del plano que equidistan de los puntos extremos de un segmento. Como consecuencia la mediatriz biseca perpendicularmente al segmento. En un triángulo, las tres mediatrices de sus lados concurren en un punto que equidista de los vértices del triángulo. El punto en el que se cortan las mediatrices de un triángulo, se conoce como circuncentro, o sea, el centro de la circunferencia circunscrita al triángulo de referencia. Al radio de la circunferencia circunscrita se le suele llamar circunradio y es la distancia desde el circuncentro a los vértices del triángulo. Obviando el rigor de la definición de círculo, a la circunferencia circunscrita se le llama también circuncírculo (para abreviar).
    
    

    

    mediatríz
    • En el triángulo ABC las mediatrices MAC, MBC y MAB se intersecan en el punto C que costituye el circucentro del triángulo o centro de la circunferencia circunscrita al triángulo ABC.
    
    

    

    Mediatrices de un triángulo rectángulo

    Mediatrices de un triángulo obtusángulo

    • En el caso de los triángulos obtusángulos, el circuncentro es un punto ubicado fuera del triángulo.
    
    

    

    Mediatrices de un triángulo obtusángulo

    Meditrices de un triángulo rectángulo

    • En el caso de los triángulos rectángulos, el circuncentro es el punto medio de la hipotenusa
      
      https://www.ecured.cu/Rectas_y_puntos_notables_de_un_tri%C3%A1ngulo

      Bisectrices, incentro y exincentros

      Las bisectrices de un triángulo son las bisectrices de sus ángulos. Existen bisectrices internas (las usuales) y externas a estos ángulos, y son perpendiculares entre sí.

      

      La bisectriz de un ángulo es el lugar geométrico de los puntos del plano que equidistan de los dos lados del ángulo.

      Las tres bisectrices interiores del triángulo (hay una por cada ángulo) se cortan en un punto que está, por tanto, a la misma distancia de los tres lados del triángulo. Eso quiere decir que se puede trazar una circunferencia con centro en dicho punto y que sea tangente a los tres lados del triángulo. A esa circunferencia se la denomina circunferencia inscrita, y al centro de la misma en el que se cortan las tres bisectrices incentro.

      Además, las bisectrices exteriores de dos ángulos concurren con la bisectriz interior del ángulo restante en puntos denominados exincentros, que son los centros de las circunferencias exinscritas del triángulo. Hay 3 exincentros, al igual que 3 circunferencias exinscritas. Las circunferencias exinscritas son tangentes a un lado y a la extensión de los otros dos.

      

      Medianas y baricentro

       Las medianas de un triángulo son las rectas que pasan por uno de sus vértices y por el punto medio del lado opuesto a dicho vértice.

      Las tres medianas de un triángulo se cortan en un punto llamado baricentro o centroide, G.

      

      Se cumple que el baricentro divide a cada mediana con razón 2:1, de manera que la distancia desde el baricentro a cada vértice es el doble que la distancia al punto medio del lado opuesto.

      

      Además, cada mediana del triángulo lo divide en dos triángulos de igual área, y las tres medianas dividen al triángulo en 6 triángulos de áreas iguales.

      También puedes observar otra cosa: uniendo los pies de las medianas (punto medio de cada lado) se obtiene un triángulo semejante al original con área 1/4 del área de éste.

      

      En algunos países a las medianas se las llama transversales de gravedad, y esto se debe a que el baricentro coincide con el centro de gravedad del triángulo. Es decir, si cortas un triángulo, por ejemplo, en una cartulina y lo sujetas colgando de un hilo justo en su baricentro, el triángulo se mantiene en equilibrio.

      Alturas y ortocentro

       Las alturas de un triángulo son las rectas que pasan por uno de sus vértices y son perpendiculares al lado opuesto de dicho vértice, o a su prolongación.

      Las tres alturas de un triángulo se cortan en un punto llamado ortocentro, H.

      

      
      

      Recta de Euler

      La recta de Euler de un triángulo es una recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo (hay otros puntos notables del triángulo que no hemos visto que también se encuentran en esta recta).

      Se denomina así en honor al matemático suizo, Leonhard Euler, quien demostró la colinealidad de los mencionados puntos notables de un triángulo, en 1765.

      

      Se cumple que la distancia del baricentro al circuncentro es la mitad de la distancia del baricentro al ortocentro. Esta es una de tantas cosas que “molan” de las matemáticas.

      https://matematicascercanas.com/2018/03/03/puntos-y-rectas-notables/
14. Polígonos regulares e irregulares
    es un concepto que procede de la lengua griega, cuyo significado puede entenderse como “muchos ángulos”. Se trata de una figura plana de la geometría que se forma a partir de la unión de segmentos rectos conocidos como lados.son aquellos cuyos lados y sus ángulos interiores resultan iguales. Esto quiere decir que todos los lados miden lo mismo, al igual que los ángulos que forman las uniones de estos segmentos.
    Estas propiedades, por otra parte, hacen que todos polígonos regulares sean polígonos equiláteros (con lados de idéntica longitud) y equiangulares(la totalidad de sus ángulos interiores miden lo mismo). Además, el polígono regular puede inscribirse en una circunferencia; esto significa que es posible dibujar una circunferencia (denominada circunscrita) que pase por todos sus puntos, de manera que la contenga completamente dentro de ella.
    https://definicion.de/poligono-regular/
    
    
    Polígono en el cual sus lados no son de igual longitud y/o sus vértices no están contenidos  en una circunferencia. De acuerdo al número de sus lados, se denominan:
    
    

    
    

                - Triángulo: polígono de 3 lados,

               - Cuadrilátero: polígono de 4 lados,

               - Pentágono: polígono de 5 lados,

               - Hexágono: polígono de 6 lados,

              - Heptágono: polígono de 7 lados,

               - Octágono: polígono de 8 lados,... y así sucesivamente.
    
    

    http://mateceblag2013.blogspot.mx/2012/11/poligonos-regulares-e-irregulares.html
15. Propiedades de los polígonos:
    A)Suma de los ángulos interiores

    Un ángulo interior es un ángulo dentro de una figura.

    
    

    Los ángulos interiores de un triángulo suman 180°
    

    http://www.disfrutalasmatematicas.com/geometria/angulos-interiores-poligonos.html
    
    

    Un ángulo interior o ángulo interno es un ángulo formado por dos lados de un polígono que comparten un vértice común, está contenido dentro del polígono.

    
    

    B)Numero de triángulos que se forma en el interior.
    
16. Perímetro y área de los polígonos
    
    
    https://www.portaleducativo.net/octavo-basico/154/Perimetro-y-area-de-poligonos
17. Fórmula de Herón
    En geometría plana elemental la fórmula de Herón, cuya invención se atribuye al matemático griego Herón de Alejandría,¹​ da el área de un triángulo conociendo las longitudes de sus tres lados a, b y c:

    ${\displaystyle {\acute {A}}rea={\sqrt {s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}}$

    donde s es el semiperímetro del triángulo:

    ${\displaystyle s={\frac {a+b+c}{2}}}$.

    Cualquier polígono simple puede ser separado en triángulos que a lo más tienen un lado común o un vértice común, mediante diagonales que parten de un único vértice apropiado. Esta subdivisión y la aplicación de la norma herodiana para el área triangular, facilita el cálculo del área de la región plana encerrada por el polígono simple, con solo medir longitudes, allí radica su importancia.
    La fórmula también puede expresarse de estas otras formas:

    ${\displaystyle {\acute {A}}rea={\ {\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)\ \over 16}}\,}}$

    ${\displaystyle {\acute {A}}rea={\ {\sqrt {2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{4}+b^{4}+c^{4})\ \over 16}}\,}}$

    ${\displaystyle {\acute {A}}rea={\ {\sqrt {(a+b+c)(a+b-c)(b+c-a)(c+a-b)\,}}\ \over 4}\,}$

    ${\displaystyle {\acute {A}}rea={\frac {1}{4}}{\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}.}$

    La fórmula de Herón se distingue de otras fórmulas para hallar el área de un triángulo, como la de la mitad de la base por la altura o la de la mitad del módulo de un producto cruz de dos lados, por no requerir ninguna elección arbitraria de un lado como base o un vértice como origen.
    https://es.wikipedia.org/wiki/F%C3%B3rmula_de_Her%C3%B3n
18. Circunferencia. Rectas y segmentos en:
    LA CIRCUNFERENCIA

    Es una línea curva cerrada y plana formada por un conjunto de puntos que equidistan de otro punto fijo llamado centro “O”, la distancia constante del centro a todos los puntos de la circunferencia recibe el nombre de radio.

    También podemos definirá a la circunferencia como el contorno o perímetro del círculo.
    

    http://solecito21roch.blogspot.mx/2012/09/la-circunferencia-sus-rectas-segmentos.html
    

    •       Centro. Es el punto fijo dentro de la circunferencia, cuya distancia a cualquier punto en el contorno es la misma.

    •       Circunferencia. Contorno exterior del circulo, también se conoce como el conjunto de puntos cuya distancia a un punto fijo, llamado centro, es la misma.

    •       Radio. Es la distancia del centro del circulo a cualquiera de los puntos de la circunferencia.

    •       Cuerda. Es el segmento de recta que une dos puntos de la circunferencia.

    •       Diámetro. Es la cuerda que pasa por el centro de la circunferencia.

    Segmentos

    •       Secante. Es la recta que corta la circunferencia en dos puntos diferentes

    •       Recta exterior.  Son todas las rectas que no cortan la circunferencia

    •       Recta tangente. Es la recta que toca la circunferencia en un solo punto

    •       Recta normal. Es una recta secante que además pasa por el centro de la circunferencia; es importante señalar que la recta tangente y la normal forman un ángulo de 90°
    

    

    http://ingluisrubin.blogspot.mx/2011/07/rectas-y-segmentos-notables-en-la.html
    
19. Ángulos en una circunferencia.
    

    Ángulo central

    Se llama ángulo central al que tiene su vértice en el centro de la circunferencia y los lados son radios de ella. En la figura está representado el ángulo  y su arco correspondiente AB. La medida angular del arco AB es la de su ángulo central . Ángulo inscrito Se llama ángulo inscrito en una circunferencia al que tiene su vértice sobre la circunferencia y sus lados la cortan. En la figura está representado el ángulo inscrito .

http://maralboran.org/wikipedia/index.php/%C3%81ngulos_en_la_circunferencia

http://maralboran.org/wikipedia/index.php/%C3%81ngulos_en_la_circunferencia