Geometría Bananosa

Glosario.

Punto

Etimología de punto

Origen, historia o formación
Proviene del latín punctum para referirse a la señal circular pequeña que divide una línea en la escritura.

https://definiciona.com/punto/

Geometría y diseño
- Punto (geometría), ente adimensional que describe una posición en el espacio;en diseño, al punto, la mínima expresión gráfica; nace con el choque de un instrumento (lápiz) contra el plano (soporte), y puede tener forma, color y textura
  
  es.wikipedia.org/wiki/Punto
Linea
La palabra línea viene del latín linea, derivada de "linum" y ésta a su vez de griego "linon" cosa hecha con lino, hilo de lino. La palabra linea es en realidad en latín el femenino del adjetivo lineus-a-um (de lino). En latín una linea se refería a un finísimo hilo de lino.
http://etimologias.dechile.net/?li.nea

Una línea está formada por una sucesión de infinitos puntos. Puede que os extrañe que sean infinitos puntos lo que la forman porque nuestra percepción visual solo ve un trazo continuo, pero si nos acercamos lo suficiente podemos apreciar que realmente son puntos que se sitúan uno junto a otro.
Linea recta
Sucesión de infinitos puntos (no tiene principio ni fin, es decir no tiene límites) donde los puntos están alineados en una misma dirección.

Si nos acercamos para ver un trozo de la línea recta con una lupa especial, vemos que efectivamente la línea está formada por puntos.

https://www.smartick.es/blog/matematicas/geometria/lineas-rectas-y-lineas-curvas/
Semirrecta
s. f. GEOMETRÍA Cada una de las dos partes en que queda dividida una recta por cualquiera de sus puntos.
https://es.thefreedictionary.com/semirrecta

Las semirrectas pueden estar abiertas o cerradas por el extremo que las delimita. El extremo que acaba en infinito o empieza en menos infinito, siempre está abierto (se utilizará el paréntesis para abrir o cerrar).

Tipos de semirrectas

Vamos a ver los diferentes tipos de semirrectas:Semirrecta abierta por la derecha

Una semirrecta abierta por la derecha:

Es el rango de valores que va desde menos infinito, hasta el extremo a, pero sin incluirlo.Comprende los números menores que a: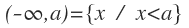

Y se representa de la siguiente forma:

Donde el punto a queda vacío.

https://ekuatio.com/intervalos-y-semirrectas/
Segmento de la linea recta
Un segmento, en geometría, es un fragmento de recta que está comprendido entre dos puntos, llamados puntos extremos o finales.

Así, dado dos puntos A y B, se le llama segmento AB a la intersección de la semirrecta de origen A que contiene al punto B con la semirrecta de origen B que contiene al punto A. Los puntos A y B son extremos del segmento y los puntos sobre la recta a la que pertenece el segmento (la «recta sostén»), serán interiores o exteriores al segmento según pertenezcan o no a este.

https://es.wikipedia.org/wiki/Segmento

Segmento AB (en verde) contenido en la recta AB.
Se caracteriza porque :
Es una porción o parte de una recta.
es la menor distancia posible entre dos puntos.
y por que tiene un principio y un final, por ende es suceptible de ser medido.

http://profesor-matematicas.blogspot.mx/2008/12/segmento-de-recta.html

Ángulo

Geometría.

Figura formada por dos segmentos de recta que inician en el mismo punto (ángulo plano) o por tres planos que se interceptan (ángulo solido).

Derivados: angular, angulado, angularmente, anguloso, angulosidad.

Espacio angular que se forma en la zona interna donde se encuentran dos paredes o dos superficies.

Sinónimo: rincón.
https://es.wiktionary.org/wiki/%C3%A1ngulo

Sistema de medición de ángulos (rados [decimal y sexagesimal] y Radiantes). Cómo convertir de grados en radiantes y de grados decimales a grados sexagesimales.
Para medir ángulos se pueden usar distintos sistemas de medición ellos son:
- Sistema Sexagesimal.
- Sistema Centesimal.
SISTEMA SEXAGESIMAL:la unidad de medida en este sistema es el grado sexagesimal (1º), que se obtiene de dividir el ángulo recto en 90 partes iguales.

1º = 1R  => 1R = 90º

   90

Los submúltiplos del grado sexagesimal son el minuto sexagesimal (1') y el segundo sexagesimal (1'').

1º = 60' ^ 1' = 60'' => 1º = 3600''

SISTEMA CENTESIMAL:  la unidad de medida en este sistema es el grado centesimal (1^G), que se obtiene de dividir el ángulo recto en 100 partes iguales.

1^G =  1R   => 1R = 100^G

   100
Los submúltiplos del grado centesimal son el minuto centesimal (1^M) y el segundo centesimal (1^S).

1^G = 100^M   ^   1^M = 100^S   ⇒   1^G = 10000^S

http://cristinabollatti.blogspot.mx/p/sistemas-de-medicion-de-angulos.html
una clasificación segun su medida es:
A)Ángulo rectoEstá compuesto por dos semirrectas que se unen por un vértice como cualquier ángulo, pero la posición de estos dos segmentos ha de ser perpendicular siempre. Al juntarse dos líneas de forma perpendicular dejan la misma separación entre una y otra, por tanto, la amplitud del ángulo recto es idéntica en cualquier caso.Dicho esto, la medida del ángulo recto será de 90 grados sin variaciones. A diferencia del ángulo agudo, del cual podemos encontrar noventa diferentes, o del ángulo obtuso con multitud de posibilidades también. Lo que hace exclusivo al ángulo recto es que siempre es igual.

https://es.plusmaths.com/angulo-recto.html
B)Ángulo agudo
El ángulo agudo es el espacio entre dos rectas que comparten un mismo vértice cuya inclinación o apertura es mayor que 0 grados (0°) y menor que 90 grados (90°).

https://www.significados.com/angulo-agudo/

c)Ángulo obtuso
Los ángulos obtusos se forman de la misma forma que los ángulos agudos o rectos, es decir, mediante dos semirrectas que se unen en un vértice. Sin embargo, se diferencian de ellos en la medida que poseen.
Los ángulos obtusos son aquellos que valen entre los 90º y los 180º. Para medir ángulos obtusos podemos hacer uso de un transportador de ángulos o mediante la combinación de la escuadra y cartabón

https://es.plusmaths.com/angulo-obtuso.html

D)Angulo llanoEs el espacio comprendido en una intersección entre dos rectas cuya apertura mide 180 grados o 180º. Como el ángulo es de 180º no hay una diferencia entre dos rectas o una recta y podemos decir que los ángulos en una línea recta siempre suman 180º.
https://www.significados.com/angulo-llano/
E)Ángulo entrante o cóncavo
Es un ángulo que oscila entre los 180º y los 360º. Es el segundo ángulo más grande después del ángulo completo.Los ángulos cóncavos también se denominan ángulos entrantes oángulos reflejos. Se llaman así también porque cuando realizamos un ángulo convexo, el ángulo resultante que se refleja por la parte exterior es un ángulo cóncavo.

https://es.plusmaths.com/angulo-concavo.html

F)Ángulo perígono.
Es el ángulo en el que uno de sus lados coincide con el otro, formando un arco de una circunferencia y cuyo valor es de 360°.
http://jorge_cetis10.mx.tripod.com/objetivo20.html
Otra clasificacion de los ángulos según su posición es:
A)Opuestos por el vértice
Los ángulos que tienen el vértice y un lado común se llaman "consecutivos".

B)Adyacentes
Se llama ángulos adyacentes a todo par de ángulos que son consecutivos y suplementarios. Los ángulos consecutivos tienen un lado común y los otros dos lados son semirrectas opuestas.

https://sites.google.com/site/susanparalela/angulos-consecutivos-adyacentes-y-opuestos-por-el-vertice

C)Complementarios
Los ángulos complementarios son aquellos ángulos cuyas medidas suman $90^{\circ }$ (grados sexagesimales), es decir que si dos ánguloscomplementarios son a su vez consecutivos, los lados no comunes de estos forman un ángulo recto.

https://es.wikipedia.org/wiki/%C3%81ngulos_complementarios

D)Suplementarios
son aquellos que suman 180º entre los dos ángulos. De esta forma son ángulos suplementarios los que, cuya suma, forma un ángulo llano, es decir 180º. El concepto de ángulo suplementario hace referencia a completar lo que le hace falta hasta que llegar a los 180º.
https://es.plusmaths.com/angulos-suplementarios.html
Triángulos
Es un polígono de tres lados que da origen a tres vértices y tres ángulos internos. Es la figura más simple, después de la recta en la geometría. Como norma general un triángulo se representa con tres letras mayúsculas de los vértices (ABC).
http://conceptodefinicion.de/triangulo/
Clasificación de los triángulos por sus lados
· Isósceles: posee dos lados iguales y uno diferente.

· Equilátero: tiene sus tres lados iguales.

· Escaleno: posee sus tres lados diferentes.
http://queenlnf.blogspot.mx/2009/04/clasificacion-de-triangulos-segun-sus.html
Clasificación de los triángulos por sus ángulos1) Rectángulos: Tienen un ángulo recto ( 90º).2 Obtusángulo: Tienen un ángulo obtuso (mas de 90º)
3) Acutángulos: Tienen todos sus ángulos agudos (menos de 90º)
http://es.tareasnormalseis.wikia.com/wiki/Clasificaci%C3%B3n_de_los_tri%C3%A1ngulos_seg%C3%BAn_sus_%C3%A1ngulos
Rectas y puntos notables en el triángulo
Entre las rectas notables más conocidas de un triángulo se pueden nombrar las mediatrices, las medianas, las alturas y las bisectrices; cada una de estas rectas notables determina cierto punto notable: circuncentro, baricentro, ortocentro e incentro, respectivamente.

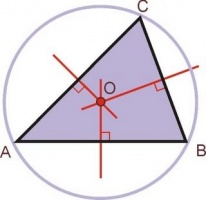
Mediatriz

Mediatriz: Conjunto de puntos del plano que equidistan de los puntos extremos de un segmento. Como consecuencia la mediatriz biseca perpendicularmente al segmento. En un triángulo, las tres mediatrices de sus lados concurren en un punto que equidista de los vértices del triángulo. El punto en el que se cortan las mediatrices de un triángulo, se conoce como circuncentro, o sea, el centro de la circunferencia circunscrita al triángulo de referencia. Al radio de la circunferencia circunscrita se le suele llamar circunradio y es la distancia desde el circuncentro a los vértices del triángulo. Obviando el rigor de la definición de círculo, a la circunferencia circunscrita se le llama también circuncírculo (para abreviar).

mediatríz
- En el triángulo ABC las mediatrices MAC, MBC y MAB se intersecan en el punto C que costituye el circucentro del triángulo o centro de la circunferencia circunscrita al triángulo ABC.
Mediatrices de un triángulo rectángulo

Mediatrices de un triángulo obtusángulo
- En el caso de los triángulos obtusángulos, el circuncentro es un punto ubicado fuera del triángulo.
Mediatrices de un triángulo obtusángulo

Meditrices de un triángulo rectángulo
- En el caso de los triángulos rectángulos, el circuncentro es el punto medio de la hipotenusa
  
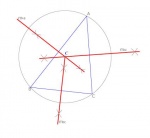
  https://www.ecured.cu/Rectas_y_puntos_notables_de_un_tri%C3%A1ngulo
  
  Bisectrices, incentro y exincentros
  
  Las bisectrices de un triángulo son las bisectrices de sus ángulos. Existen bisectrices internas (las usuales) y externas a estos ángulos, y son perpendiculares entre sí.
  
  La bisectriz de un ángulo es el lugar geométrico de los puntos del plano que equidistan de los dos lados del ángulo.
  
  Las tres bisectrices interiores del triángulo (hay una por cada ángulo) se cortan en un punto que está, por tanto, a la misma distancia de los tres lados del triángulo. Eso quiere decir que se puede trazar una circunferencia con centro en dicho punto y que sea tangente a los tres lados del triángulo. A esa circunferencia se la denomina circunferencia inscrita, y al centro de la misma en el que se cortan las tres bisectrices incentro.
  
  Además, las bisectrices exteriores de dos ángulos concurren con la bisectriz interior del ángulo restante en puntos denominados exincentros, que son los centros de las circunferencias exinscritas del triángulo. Hay 3 exincentros, al igual que 3 circunferencias exinscritas. Las circunferencias exinscritas son tangentes a un lado y a la extensión de los otros dos.
  
  Medianas y baricentro
  
  Las medianas de un triángulo son las rectas que pasan por uno de sus vértices y por el punto medio del lado opuesto a dicho vértice.
  
  Las tres medianas de un triángulo se cortan en un punto llamado baricentro o centroide, G.
  
  Se cumple que el baricentro divide a cada mediana con razón 2:1, de manera que la distancia desde el baricentro a cada vértice es el doble que la distancia al punto medio del lado opuesto.
  
  Además, cada mediana del triángulo lo divide en dos triángulos de igual área, y las tres medianas dividen al triángulo en 6 triángulos de áreas iguales.
  
  También puedes observar otra cosa: uniendo los pies de las medianas (punto medio de cada lado) se obtiene un triángulo semejante al original con área 1/4 del área de éste.
  
  En algunos países a las medianas se las llama transversales de gravedad, y esto se debe a que el baricentro coincide con el centro de gravedad del triángulo. Es decir, si cortas un triángulo, por ejemplo, en una cartulina y lo sujetas colgando de un hilo justo en su baricentro, el triángulo se mantiene en equilibrio.
  
  Alturas y ortocentro
  
  Las alturas de un triángulo son las rectas que pasan por uno de sus vértices y son perpendiculares al lado opuesto de dicho vértice, o a su prolongación.
  
  Las tres alturas de un triángulo se cortan en un punto llamado ortocentro, H.
  
  Recta de Euler
  
  La recta de Euler de un triángulo es una recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo (hay otros puntos notables del triángulo que no hemos visto que también se encuentran en esta recta).
  
  Se denomina así en honor al matemático suizo, Leonhard Euler, quien demostró la colinealidad de los mencionados puntos notables de un triángulo, en 1765.
  
  Se cumple que la distancia del baricentro al circuncentro es la mitad de la distancia del baricentro al ortocentro. Esta es una de tantas cosas que “molan” de las matemáticas.
  
  https://matematicascercanas.com/2018/03/03/puntos-y-rectas-notables/
Polígonos regulares e irregulares
es un concepto que procede de la lengua griega, cuyo significado puede entenderse como “muchos ángulos”. Se trata de una figura plana de la geometría que se forma a partir de la unión de segmentos rectos conocidos como lados.son aquellos cuyos lados y sus ángulos interiores resultan iguales. Esto quiere decir que todos los lados miden lo mismo, al igual que los ángulos que forman las uniones de estos segmentos.
Estas propiedades, por otra parte, hacen que todos polígonos regulares sean polígonos equiláteros (con lados de idéntica longitud) y equiangulares(la totalidad de sus ángulos interiores miden lo mismo). Además, el polígono regular puede inscribirse en una circunferencia; esto significa que es posible dibujar una circunferencia (denominada circunscrita) que pase por todos sus puntos, de manera que la contenga completamente dentro de ella.

https://definicion.de/poligono-regular/

Polígono en el cual sus lados no son de igual longitud y/o sus vértices no están contenidos  en una circunferencia. De acuerdo al número de sus lados, se denominan:

  - Triángulo: polígono de 3 lados,

- Cuadrilátero: polígono de 4 lados,
- Pentágono: polígono de 5 lados,
- Hexágono: polígono de 6 lados,
  - Heptágono: polígono de 7 lados,
- Octágono: polígono de 8 lados,... y así sucesivamente.

http://mateceblag2013.blogspot.mx/2012/11/poligonos-regulares-e-irregulares.html
Propiedades de los polígonos:

A)Suma de los ángulos interiores

Un ángulo interior es un ángulo dentro de una figura.

Los ángulos interiores de un triángulo suman 180°
http://www.disfrutalasmatematicas.com/geometria/angulos-interiores-poligonos.html

Un ángulo interior o ángulo interno es un ángulo formado por dos lados de un polígono que comparten un vértice común, está contenido dentro del polígono.

B)Numero de triángulos que se forma en el interior.
Perímetro y área de los polígonos

https://www.portaleducativo.net/octavo-basico/154/Perimetro-y-area-de-poligonos
Fórmula de Herón
En geometría plana elemental la fórmula de Herón, cuya invención se atribuye al matemático griego Herón de Alejandría,¹ da el área de un triángulo conociendo las longitudes de sus tres lados a, b y c:

${\acute {A}}rea={\sqrt {s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}$

donde s es el semiperímetro del triángulo:

$s={\frac {a+b+c}{2}}$ .

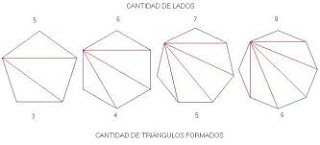
Cualquier polígono simple puede ser separado en triángulos que a lo más tienen un lado común o un vértice común, mediante diagonales que parten de un único vértice apropiado. Esta subdivisión y la aplicación de la norma herodiana para el área triangular, facilita el cálculo del área de la región plana encerrada por el polígono simple, con solo medir longitudes, allí radica su importancia.

La fórmula también puede expresarse de estas otras formas:

${\acute {A}}rea={\ {\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)\ \over 16}}\,}$

${\acute {A}}rea={\ {\sqrt {2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{4}+b^{4}+c^{4})\ \over 16}}\,}$

${\acute {A}}rea={\ {\sqrt {(a+b+c)(a+b-c)(b+c-a)(c+a-b)\,}}\ \over 4}\,$

${\acute {A}}rea={\frac {1}{4}}{\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}.$

La fórmula de Herón se distingue de otras fórmulas para hallar el área de un triángulo, como la de la mitad de la base por la altura o la de la mitad del módulo de un producto cruz de dos lados, por no requerir ninguna elección arbitraria de un lado como base o un vértice como origen.

https://es.wikipedia.org/wiki/F%C3%B3rmula_de_Her%C3%B3n
Circunferencia. Rectas y segmentos en:

LA CIRCUNFERENCIA
Es una línea curva cerrada y plana formada por un conjunto de puntos que equidistan de otro punto fijo llamado centro “O”, la distancia constante del centro a todos los puntos de la circunferencia recibe el nombre de radio.

También podemos definirá a la circunferencia como el contorno o perímetro del círculo.
http://solecito21roch.blogspot.mx/2012/09/la-circunferencia-sus-rectas-segmentos.html

•       Centro. Es el punto fijo dentro de la circunferencia, cuya distancia a cualquier punto en el contorno es la misma.

•       Circunferencia. Contorno exterior del circulo, también se conoce como el conjunto de puntos cuya distancia a un punto fijo, llamado centro, es la misma.

•       Radio. Es la distancia del centro del circulo a cualquiera de los puntos de la circunferencia.

•       Cuerda. Es el segmento de recta que une dos puntos de la circunferencia.

•       Diámetro. Es la cuerda que pasa por el centro de la circunferencia.

Segmentos

•       Secante. Es la recta que corta la circunferencia en dos puntos diferentes

•       Recta exterior.  Son todas las rectas que no cortan la circunferencia

•       Recta tangente. Es la recta que toca la circunferencia en un solo punto

•       Recta normal. Es una recta secante que además pasa por el centro de la circunferencia; es importante señalar que la recta tangente y la normal forman un ángulo de 90°

http://ingluisrubin.blogspot.mx/2011/07/rectas-y-segmentos-notables-en-la.html

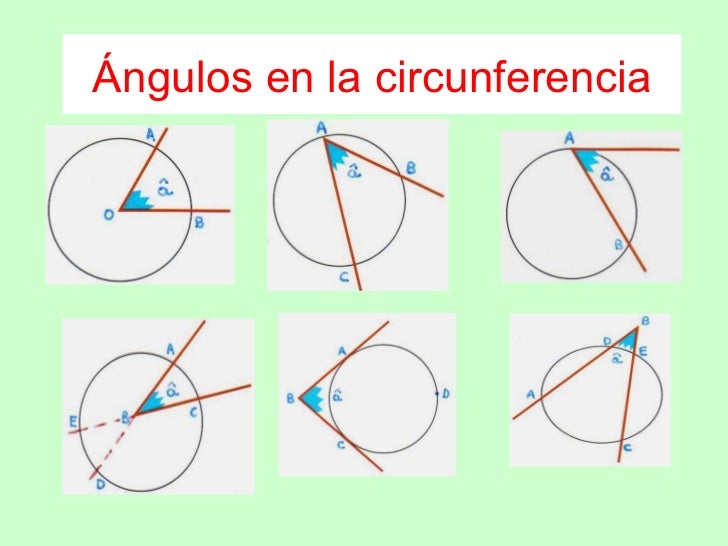
Ángulos en una circunferencia.
Ángulo central

Se llama ángulo central al que tiene su vértice en el centro de la circunferencia y los lados son radios de ella.
En la figura está representado el ángulo $\widehat{AOB}$ y su arco correspondiente AB.

La medida angular del arco AB es la de su ángulo central $\widehat{AOB}$ .

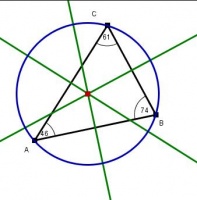
Ángulo inscrito

Se llama ángulo inscrito en una circunferencia al que tiene su vértice sobre la circunferencia y sus lados la cortan.
En la figura está representado el ángulo inscrito $\widehat{BAC}$ .